K近邻法与k-means
简介
K近邻法(knn)是一种基本的分类与回归方法。k-means是一种简单而有效的聚类方法。虽然两者用途不同、解决的问题不同,但是在算法上有很多相似性,于是将二者放在一起,这样能够更好地对比二者的异同。
算法描述
knn
算法思路:
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
k近邻模型的三个基本要素:
- k值的选择:k值的选择会对结果产生重大影响。较小的k值可以减少近似误差,但是会增加估计误差;较大的k值可以减小估计误差,但是会增加近似误差。一般而言,通常采用交叉验证法来选取最优的k值。
- 距离度量:距离反映了特征空间中两个实例的相似程度。可以采用欧氏距离、曼哈顿距离等。
- 分类决策规则:往往采用多数表决。
k-means
算法步骤:
- 从n个数据中随机选择 k 个对象作为初始聚类中心;
- 根据每个聚类对象的均值(中心对象),计算每个数据点与这些中心对象的距离;并根据最小距离准则,重新对数据进行划分;
- 重新计算每个有变化的聚类簇的均值,选择与均值距离最小的数据作为中心对象;
- 循环步骤2和3,直到每个聚类簇不再发生变化为止。
k-means方法的基本要素:
- k值的选择:也就是类别的确定,与K近邻中k值的确定方法类似。
- 距离度量:可以采用欧氏距离、曼哈顿距离等。
应用实例
问题描述
已知若干人的性别、身高和体重,给定身高和体重判断性别。考虑使用k近邻算法实现性别的分类,使用k-means实现性别的聚类。
数据
数据集合:https://github.com/shuaijiang/FemaleMaleDatabase
该数据集包含了训练数据集和测试数据集,考虑在该数据集上利用k近邻算法和k-means方法分别实现性别的分类和聚类。
将训练数据展示到图中,可以更加直观地观察到数据样本之间的联系和差异,以及不同性别之间的差异。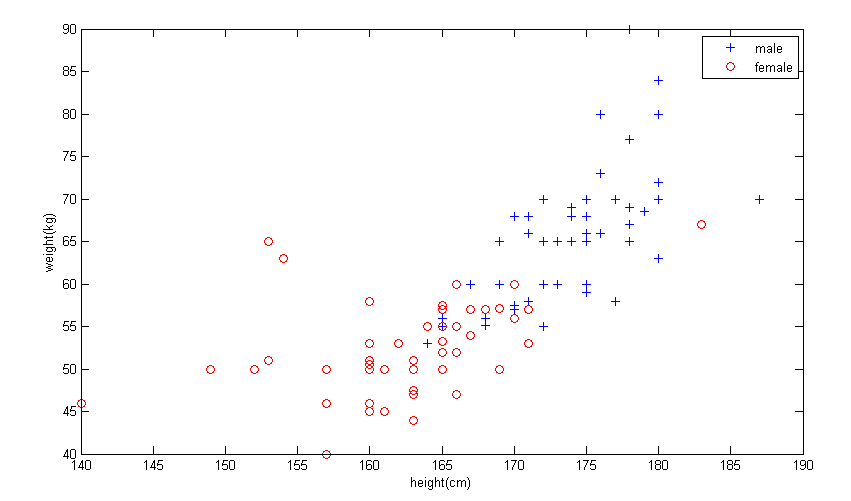
KNN的分类结果
KNN算法中的基本设置
- k=5
- 距离度量:欧氏距离
- 分类决策规则:多数投票
- 测试集:https://github.com/shuaijiang/FemaleMaleDatabase/blob/master/test0.txt
利用KNN算法,在测试集上的结果如下混淆矩阵表所示。从表中可以看出,测试集中的男性全部分类正确,测试集中的女性有一个被错误分类,其他都分类正确。
混淆矩阵 Test:male Test:female Result:male 20 1 Result:female 0 14
(表注:Test:male、Test:female分别表示测试集中的男性和女性,Result:male和Result:female分别表示结果中的男性和女性。表格中第一个元素:即Test:male列、Result:male行,表示测试集中为男性、并且结果中也为男性的数目。表格中其他元素所代表的含义以此类推)
由上表可以计算分类的正确率:(20+14)/(20+14+1) = 97.14%
K-means的聚类结果
K-means算法的基本设置
- k=2
- 距离度量:欧氏距离
- 最大聚类次数:200
- 类别决策规则:根据每个聚类簇中的多数决定类别
- 测试集:https://github.com/shuaijiang/FemaleMaleDatabase/blob/master/test0.txt
混淆矩阵 Test:male Test:female Result:male 20 1 Result:female 0 14
(表注:该表与上表内容一致)
由于选择初始中心点是随机的,所以每次的聚类结果都不相同,最好的情况下能够完全聚类正确,最差的情况下两个聚类簇没有分开,根据多数投票决定类别时,被标记为同一个类别。
KNN VS K-means
二者的相同点:
- k的选择类似
- 思路类似:根据最近的样本来判断某个样本的属性
二者的不同点:
- 应用场景不同:前者是分类或者回归问题,后者是聚类问题;
- 算法复杂度: 前者O(n^2),后者O(kmn);(k是聚类类别数,m是聚类次数)
- 稳定性:前者稳定,后者不稳定。
总结
本文概括地描述了K近邻算法和K-means算法,具体比较了二者的算法步骤。在此基础上,通过将两种方法应用到实际问题中,更深入地比较二者的异同,以及各自的优劣。本文作者还分别实现了K近邻算法和K-means算法,并且应用到了具体问题上,最后得到了结果。
以上内容难免有所纰漏和错误,欢迎指正。
源代码
参考文献
- 李航. 统计学习方法.清华大学出版社.2012