朴素贝叶斯（naive Bayes）

简介

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。其基本的思路是：对于给定的训练数据集，首先基于特征条件独立假设学习输入和输出的联合概率分布，然后基于该模型，对于给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。
朴素贝叶斯法实现简单，学习和预测的效率都很高，是一种比较常用的方法。

朴素贝叶斯法

朴素贝叶斯法是典型的生成学习方法。
输入空间$X$，输出空间$Y$，由训练数据学习联合概率分布$P(X,Y)$，然后求得后验概率分布$P(Y|X)$

条件独立性假设

条件概率分布
$P(X=x|Y=c_k)=P(X^{(1)}=x^{(1)},\ldots,X^{(n)}=x^{(n)}|Y=c_k), k=1,2,\ldots,K$

朴素贝叶斯法对条件概率分布作了条件独立性的假设：
$P(X=x|Y=c_k)$

$=P(X^{(1)}=x^{(1)},\ldots,X^{(n)}=x^{(n)}|Y=c_k)$

$=\prod^n_{j=1} P(X^{(j)}|Y=c_k)$
由于这一假设，模型的条件概率的数量大为减少，朴素贝叶斯法的学习与预测就简化了很多，并且容易实现。然而，这也导致分类的性能不是很高。

贝叶斯定理

朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测。

$P(Y|X) = \frac{P(X,Y)}{P(X)}=\frac{P(Y)P(X|Y)}{\sum_YP(P(Y)P(X|Y))}$

对输入x得到后验概率最大的类y

$y=\arg \max_{c_k}P(Y=c_k)P(X_j=x^{(j)}|Y=c_k)$

$y=\arg \max_{c_k}P(Y=c_k) \prod_j P(X_j=x^{(j)}|Y=c_k)$

朴素贝叶斯法的参数估计

概率估计方法有两种：极大似然估计；贝叶斯估计。

极大似然估计

先验概率$P(Y=c_k)$的极大似然估计
$P(Y=c_k)=\frac{\sum^N_i I(y_i=c_i)}{N},k=1,2,\ldots,K$

贝叶斯估计

应用实例

问题描述

已知若干人的性别、身高和体重，给定身高和体重判断性别。考虑使用朴素贝叶斯法实现性别的分类。

数据

数据集合：https://github.com/shuaijiang/FemaleMaleDatabase

该数据集包含了训练数据集和测试数据集，考虑在该数据集上利用朴素贝叶斯法实现性别的分类。

将训练数据展示到图中，可以更加直观地观察到数据样本之间的联系和差异，以及不同性别之间的差异。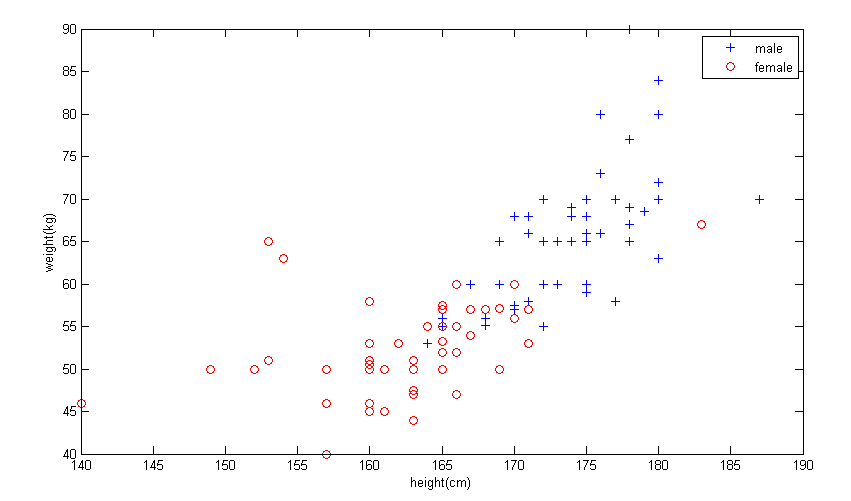

朴素贝叶斯的分类结果

源代码

朴素贝叶斯源代码：https://github.com/shuaijiang/naive_bayes

参考文献

1. 李航. 统计学习方法.清华大学出版社.2012