机器学习概述
简介
机器学习就是将数据转变成信息。机器学习一般采用统计方法,由数据驱动,从数据中提取特征、抽象出模型、发现数据中的知识,最终应用到数据的分析和预测。
统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测与分析的一门学科。
统计学习的三要素
- 模型
- 策略
- 算法
模型
学习什么样的模型是统计学习首先考虑的问题。在监督学习过程中,模型就是所要学习的条件概率分布或决策函数。模型的假设空间包含所有可能的条件概率分布或决策函数。
模型空间可以定义为条件概率的集合,也可以定义为决策函数的集合。
用S表示模型空间,条件概率的集合可以表示为$S=\lbrace P|P(Y|X)\rbrace$,其中,X和Y分别是定义在输入空间和输出空间的随机变量。这时$S$通常是由一个参数向量决定的条件概率分布族:$S=\lbrace P|P_{\theta} (Y|X),\theta \in R^n \rbrace$,参数向量$\theta$取决于n维欧式空间$R^n$,也称为参数空间。
类似的,决策函数的集合可以表示为$S=\lbrace f|Y=f(X)\rbrace$,其中,X和Y分别是定义在输入空间和输出空间的变量。这时$S$通常是由一个参数向量决定的函数族:$S=\lbrace f|f_{\theta} (X),\theta \in R^n \rbrace$,参数向量$\theta$取决于n维欧式空间$R^n$,也称为参数空间。
由决策函数表示的模型称为非概率模型,由条件概率表示的模型称为概率模型。
策略
选择最优模型是统计学习的目标,策略是选择最优模型的准则。损失函数度量模型一次预测的好坏,风险函数度量平均意义下模型预测的好坏。
损失函数和风险函数
常用的损失函数有下面的几种:
- 0-1损失函数:
$L(Y,f(X))= 1, Y \ne f(X) $ ; $ L(Y,f(X))= 0, Y = f(X)$ - 平方损失函数:
$L(Y,f(X)) = (Y-f(X))^2$ - 绝对损失函数:
$L(Y,f(X)) = |Y-f(X)|$ - 对数损失函数:
$L(Y,f(X)) = - \lg P(Y|X)$
风险函数(或称期望损失),是模型$f(X)$关于联合分布$P(X,Y)$的平均意义下的损失:
$R(f) = E_p [L(Y,f(X))]= \int L(y,f(x)) P(x,y) dxdy$
学习的目标就是选择期望风险最小的模型。但是联合分布$P(X,Y)$是未知的,所以不能直接计算期望风险。
经验风险(或称经验损失),是模型$f(X)$关于训练数据集的平均损失:
$R(f) = \frac{1}{N} \sum L(y_i,f(x_i))$
期望风险是模型关于联合分布的期望损失,经验风险是模型关于训练样本集的平均损失。根据大数定律,当样本容量$N$趋于无穷时,经验风险趋于期望风险,所以可以用经验风险来估计期望风险。
经验风险最小化与结构风险最小化
经验风险最小化的策略认为,经验风险最小的模型是最优的模型。经验风险最小化也就是求解最优化问题:
$\min_{f \in F} \frac{1}{N} \sum L(y_i,f(x_i))$
极大似然估计是经验风险最小化的一个例子。但是,当样本容量很小时,经验风险最小化学习的效果不一定会好,会产生过拟合现象。
为了防止过拟合提出结构风险最小化策略,其等价于正则化,结构风险在经验风险上增加了表示模型复杂度的正则化项。结构风险的定义是:
$R(f) = \frac{1}{N} \sum L(y_i,f(x_i)) + \lambda J(f)$
结构风险最小化的策略认为,结构风险最小的模型是最优的模型。最大后验概率估计是结构风险最小化的一个例子。
算法
算法是学习模型的具体计算方法。统计学习基于训练数据集,根据学习策略,从假设空间中选择最优模型,最后需要考虑用什么样的计算方法求解最优模型。
也就是,统计学习问题归结为最优化问题,统计学习的算法成为求解最优化问题的算法。
模型评估与模型选择
统计学习的目的是使学到的模型不仅对已知的数据而且对未知数据都能有很好的预测能力。一般而言,使用训练误差和测试误差分别来衡量对已知和未知数据的预测能力。
训练误差和测试误差
当损失函数给定时,基于损失函数的模型的训练误差和模型的测试误差就成为学习方法评估的标准。
假设已经学习到的模型是$Y=\hat{f}(X)$,训练误差是模型关于训练数据集的平均损失:
$R_{emp} (\hat{f}) = \frac{1}{N} \sum_i ^{N} L(y_i,\hat{f}(x_i))$
测试误差是模型关于测试数据集的平均损失:
$e_{test} = \frac{1}{N’} \sum_i ^{N’} L(y_i,\hat{f}(x_i))$
训练误差的大小,对判断问题是不是一个容易学习的问题是有意义的,但是本质上并不重要。测试误差反映了学习方法对未知的测试数据集的预测的能力,是学习中的重要概念。给定不同的学习方法,测试误差小的方法具有更好的预测能力,是更有效的方法。
过拟合与模型选择
当参数空间有不同复杂度的模型时,就要面临模型选择的问题。我们希望选择或者学习到一个合适的模型,应该逼近真模型。也就是,所选择的模型要与真模型的参数个数相同、参数向量相近。
如果一味追求提高对训练数据的预测能力,所选模型复杂度则往往会比真实模型要高,这种现象就是过拟合(over-fitting)。具体来说,过拟合是指学习时选择的模型所包含的参数过多,以致于出现模型对已知数据预测得很好,但对未知数据预测得很差的现象。
下图描述了训练误差和测试误差与模型复杂度的关系:当模型的复杂度增大时,训练误差会逐渐减小并趋于0;而测试误差会先减小,达到最小值之后又增大。当选择的模型复杂度过大时,过拟合现象就会发生。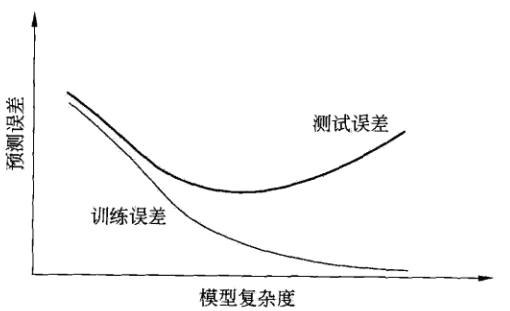
生成模型与判别模型
监督学习方法可以分为:生成方法(generative approach)和判别方法(discriminative approach),所学到的模型分别称为生成模型和判别模型。
生成方法有数据学习联合概率分布$P(X,Y)$,然后求出条件概率分布最为预测的模型,即生成模型: $P(Y|X) = \frac{P(X,Y)}{P(X)}$。
典型的生成方法包括:朴素贝叶斯法和隐马尔科夫模型。
生成方法的特点:
- 生成方法可以还原出联合概率分布$P(X,Y)$, 而判别方法则不能;
- 生成方法的学习收敛速度更快,即当样本容量增加的时候,学到的模型可以更快地收敛于真实的模型;
- 当存在隐变量的时候,仍可以用生成方法学习,此时判别方法就不能用。
判别方法由数据直接学习决策函数$f(X)$或者条件概率分布$P(Y|X)$作为预测的模型,即判别模型。
典型的判别方法包括:k近邻法、感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机、
提升方法和条件随机场等。
判别方法的特点:
- 判别方法学习的是条件概率$P(Y|X)$或决策函数$f(X)$,直接面对预测,往往学习的准确率更高;
- 由于直接学习$P(Y|X)$或$f(X)$,可以对数据进行各种程度上的抽象、定义特征并使用特征,因此可以简化学习问题。
分类问题
分类是监督学习的一个核心问题。在监督学习中,当输出变量Y取有限个离散值时,预测问题便成为分类问题。
可以用于分类的统计学习方法包括:k近邻法、感知机、朴素贝叶斯法、决策树、决策列表、逻辑斯蒂回归模型、支持向量机、提升方法、贝叶斯网络、神经网络等。
标注问题
标注问题的输入是一个观测序列,输出是一个标记序列或状态序列。
标注常用的统计学习方法有:隐马尔科夫模型、条件随机场。
回归问题
回归(regression)用于预测输入变量和输出变量之间的关系。回归问题的学习等价于函数拟合:选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。
参考文献
- 李航.统计学习方法.清华大学出版社.2012
- Peter Harrington.机器学习实战.人民邮电出版社.2013